Fundamentals of Computer Graphics, Fourth Edition¶
第一章:简介¶
- 1.6:效率
- 比起运算次数,程序员应当更加重视访存模式,因为如今内存速度跟不上处理器。
- 提高局部性,尝试使数据结构的大小与目标体系结构的内存页面、缓存行大小相适配。
- 当心老旧的优化建议,可能已经不再适用。
- 一定要做 Profiling。
-
1.7:图形程序的设计和编程
-
一些基本的数据结构:
-
还介绍了图形程序中常用的调试技术。对于图形程序来说,调试器基本没什么用,输出的图像本身是最好的调试信息。比如,可以在某个阶段把像素直接拷贝到屏幕上,以检测后面阶段的问题。
-
第二章:数学大杂烩¶
The cleaner the math, the cleaner the resulting code.
本章内容包括:
- 集合与映射
- 求解二次方程
- 三角函数
- 向量
- 曲线和曲面
- 线性插值
- 三角形
让我们直接从曲面开始:
曲面¶
- 三维曲面:\(f(\mathbf{p}) = 0\)。
- 法向量(normal vector):\(\mathbf{n} = \nabla f(\mathbf{p}) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)\),指向 \(f(\mathbf{p}) > 0\) 的方向。
- 三维平面:
- \((\mathbf{p} - \mathbf{a}) \cdot \mathbf{n} = 0\)。
- \((\mathbf{p} - \mathbf{a}) \cdot ((\mathbf{b} - \mathbf{a}) \times (\mathbf{c} - \mathbf{a})) = 0\)。
- \(\begin{vmatrix} x - x_a & y - y_a & z - z_a \\ x_b - x_a & y_b - y_a & z_b - z_a \\ x_c - x_a & y_c - y_a & z_c - z_a \end{vmatrix} = 0\)。
- 三维曲线:使用曲面的交集表示,\(f(\mathbf{p}) = 0\) 和 \(g(\mathbf{p}) = 0\)。
- 二维参数化曲线:\(\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x(t) \\ y(t) \end{bmatrix}\) 或者表示为向量函数 \(\mathbf{p} = f(t)\)。
- 直线:\(\mathbf{p}(t) = \mathbf{o} + t (\mathbf{d}\))。
- 椭圆:\(\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x_c + a \cos \phi \\ y_c + b \sin \phi \end{bmatrix}\)。
- 三维参数化曲线:\(\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \mathbf{p}(t)\)。
- 三维参数化曲面:\(\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \mathbf{p}(u, v)\)。
- 曲面上的等值曲线(isoparametric curve):\(\mathbf{q}(t) = \mathbf{p}(t, v_0)\)。
- 法向量 \(\mathbf{n} = \mathbf{p}_u \times \mathbf{p}_v\)。
- 总结:
- 隐式二维曲线、三维曲面:\(S=\{\mathbf{p}|f(\mathbf{p})=0\}\),\(f\) 是 \(\mathbb{R}^3\) 或 \(\mathbb{R}^2 \to \mathbb{R}\)。法向量由 \(f\) 的导数(梯度)给出,用法向量构建基底得到切向量或切平面。
- 二维、三维参数化曲线:\(S=\{\mathbf{p}(t) | t \in D\}\)。\(\mathbf{p}\) 的导数给出切向量(tangent vector)。
- 参数化曲面:\(S=\{\mathbf{p}(u, v) | (u, v) \in D\}\)。
线性插值¶
三角形¶
三角形是二维和三维建模的原语(primitive)。颜色等信息标记在顶点,在三角形内部插值,这样的坐标系称为质心坐标系(barycentric coordinates)。
- 法向量:\(\mathbf{n} = (\mathbf{b} - \mathbf{a}) \times (\mathbf{c} - \mathbf{a})\)。
以三角形的两条边为基底,可以构建质心坐标系:
要计算任意一点的质心坐标其实很容易,因为 \(f(x,y)\) 表明该点到直线的距离(按某比例缩放),再与三角形顶点的距离做比值即可。如:\(\beta = \frac{f_{ac}(x, y)}{f_{ac}(x_b, y_b)}\)。通常计算其中两个,用和为 1 计算最后一个参数。
相同的道理,还可以使用面积比例计算质心坐标。
注意到法向量的长度是三角形的面积的两倍,上式又可以用法向量表示:
第三章:栅格化图像¶
像素与几何¶
- 伽马值
- 人眼对亮度的感知是非线性的,显示器的输出相较于输入也是非线性的。
- 通常用该式拟合 \(\text{displayed intensity} = (\text{maximum intensity})a^\gamma\)。
RGB 颜色空间¶
显示器领域使用三原色为 RGB,称为叠加混合(additive mixing),与出版业的 CMYK 颜色空间不同,CMYK 是减色混合(subtractive mixing)。这很容易理解,因为显示器是发光体,而印刷品是反射体,前者主动发光,后者靠吸收光线和反射光线来表现颜色。
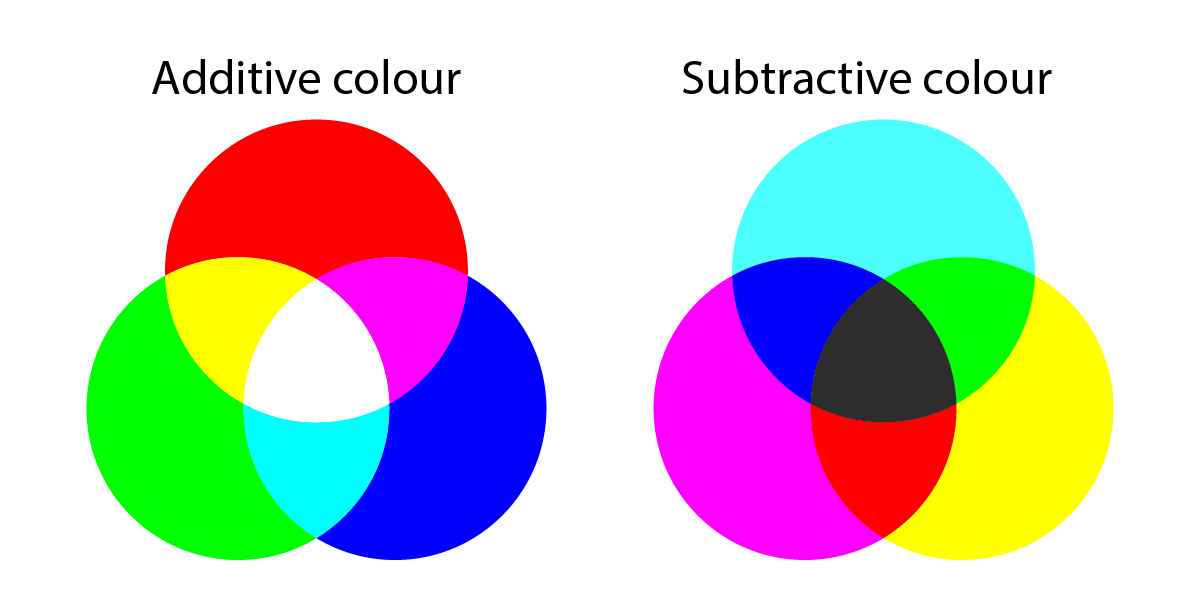
Colour Theory: Understanding and Working with Colour - RMIT
颜色生词表:
| 英文 | 中文 | CSS 颜色 |
|---|---|---|
| magenta | 洋红 | magenta |
| cyan | 青色 | cyan |
Alpha 混合¶
分别为前景色(foreground)和背景色(background)。
第四章:光线追踪¶
简单光线追踪算法¶
渲染的过程就是接收一组物体,产生二维图像。
两种渲染顺序:
- 物体顺序(object-order):逐个物体渲染,更新影响的像素。
- 图像顺序(image-order):逐个像素渲染,考虑所有物体。
这两种顺序用于不同效果,性能也不同。
光线追踪是一种图像顺序算法。从观察者的视角出发,每个像素看向不同地方,目标是找到该视线所看到的物体。找到视线与物体的交点后,着色器使用交点、表面法向量和其他信息确定像素的颜色。光线追踪器包含三个部分:
- 光线生成器:确定视线的起点和方向。
- 光线求交器:找到视线与物体的交点。
- 着色器:确定像素的颜色。
for each pixel (x, y) {
generate ray r from eye through (x, y)
find first intersection i of r with scene
set pixel (x, y) to color of i
}
透视¶
- 平行投影(parallel projection):视线是平行的。若投影面与投影线垂直,所得图像是正交的(orthographic),否则为斜交的(oblique)。
- 透视投影(perspective projection):视线收敛于一点,所得图像是透视的(perspective)。
在艺术中,使用三点透视法(three-point perspective)。有趣的是,只要使用透视投影,三点透视法的条件就自然满足。
计算视线¶
三维参数化曲线很适合描述视线。令视点(viewpoint 或 eye point)为 \(e\),所看点为 \(s\),则视线表示为
相机坐标系三个向量组成右手系:
- \(\mathbf{u}\):指向右侧。
- \(\mathbf{v}\):指向上方。
- \(\mathbf{w}\):指向后方。
观察方向为 \(-\mathbf{w}\)。
| 投影方式 | 光线方向 | 光线起点 |
|---|---|---|
| 正交投影 | \(-\mathbf{w}\) | \(e + u\mathbf{u} + v\mathbf{v}\) |
| 透视投影 | \(-d\mathbf{w} + u\mathbf{u} + v\mathbf{v}\) | \(e\) |
其中焦距 \(d\) 为视点 \(e\) 与投影面的距离。
光线求交¶
直接代入即可:
对于参数化曲面:
三角形是平面图形,上式换成平面方程:
- 解出 \(t, \beta, \gamma\)。
- 如果满足 \(\beta > 0, \gamma > 0, \beta + \gamma < 1\),则交点在三角形内部。
平面多边形具有顶点 \(\mathbf{p}_1 \ldots \mathbf{p}_n\) 和法向量 \(\mathbf{n}\)。
- 计算光线与平面交点:\((\mathbf{p} - \mathbf{p}_1) \cdot \mathbf{n} = 0\) 得到 \(t\)。
-
将交点和平面多边形投影到 \(xy\) 平面上,判断是否在多边形内部。
- 最简单的方法是从该点发出一条射线,计算与多边形的交点数。奇数个交点则在内部,偶数个交点则在外部。
- 另一种方法是用多个三角形拼接多边形,转化为点是否在三角形内部的问题。
- 如果投影到 \(xy\) 平面是一条线,我们可以选用其他平面,如 \(yz\)、\(zx\) 平面。
着色¶
计算光的反射需要光线方向 \(\mathbf{l}\)、法向量 \(\mathbf{n}\) 和视线方向 \(\mathbf{v}\)。本节的着色算法对每个颜色通道分别计算。
- Lambertian Shading:
- 像素颜色 \(L=k_d I \max(0, \mathbf{n} \cdot \mathbf{l})\)。\(k_d\) 为漫反射系数(diffuse coefficient),\(I\) 为光强。
- 效果是哑光的,表面的颜色与视角无关,无法表现高光等效果。
- Blinn-Phong Shading:
- 在 Lambertian Shading 的基础上加入镜面部分(specular component),前者成为漫反射部分(diffuse component)。
- 半向量 \(\mathbf{h} = \frac{\mathbf{l} + \mathbf{v}}{||\mathbf{l} + \mathbf{v}||}\) 是光线和视线的平分线。比较它和法向量的夹角,夹角越小,镜面反射越强。
- 像素颜色 \(L = k_d I \max(0, \mathbf{n} \cdot \mathbf{l}) + k_s I \max(0, \mathbf{n} \cdot \mathbf{h})^n\)。\(k_s\) 为镜面反射系数(specular coefficient),\(p\) 为高光系数。
- Ambient Shading:
- 为了避免黑暗区域,我们加入环境光(ambient light)。
- 像素颜色 \(L = k_a I_a + k_d I \max(0, \mathbf{n} \cdot \mathbf{l}) + k_s I \max(0, \mathbf{n} \cdot \mathbf{h})^n\)。\(k_a\) 为环境光系数(ambient coefficient),\(I_a\) 为环境光强。
- 多点光源:\(L = k_a I_a + \sum_{i=1}^n [k_d I_i \max(0, \mathbf{n} \cdot \mathbf{l}_i) + k_s I_i \max(0, \mathbf{n} \cdot \mathbf{h}_i)^n]\)。
光线追踪程序¶
展示了使用面向对象的方法写一个简单的光线追踪程序。
阴影¶
从交点沿光线入射反方向发射光线 \(\mathbf{p} + t\mathbf{l}\),如果遇到物体,则交点在阴影中。该射线称为阴影射线(shadow ray),与观测射线(view ray)区分。
数值问题
可能计算到 \(p\) 点表面附近的区域,因此从 \(\mathbf{p} + \epsilon\mathbf{l}\) 开始发射阴影射线。
理想镜面反射¶
加入一次递归的光线追踪:
为什么是递归?
因为光线就是递归的。
需要注意的是,递归可能永远不会停下。此时需要加入最大递归深度进行限制。
第五章:线性代数¶
Todo
第六章:变换矩阵¶
二维线性变换¶
简单列一下:
- 缩放 \(S = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}\)
- 剪切(shear 或 tilt) \(S = \begin{bmatrix} 1 & t_x \\ t_y & 1 \end{bmatrix}\) 或 \(S = \begin{bmatrix} 1 & \tan(\phi) \\ \tan(\theta) & 1 \end{bmatrix}\)
- 旋转 \(S = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}\)
- 翻转 \(S = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\) 或 \(S = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)
重要的是 6.1.6 节变换的分解:
- 任何二维线性变换都可以分解为旋转、缩放、旋转的乘积。
- 对称特征值分解:对称矩阵总是能使用特征分解分解为 \(\mathbf{A}=\mathbf{RSR}^T\),其中 \(R\) 是正交矩阵,\(S\) 是对角矩阵。
- 奇异值分解:非对称矩阵使用 SVD 分解为 \(\mathbf{A}=\mathbf{USV}^T\),其中 \(\mathbf{U}\) 和 \(\mathbf{V}\) 是正交矩阵,\(\mathbf{S}\) 是对角矩阵。
三维线性变换¶
- 缩放:\(\text{scale}(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix}\)
- 旋转:
- 绕 x 轴:\(\text{rotate-x}(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{bmatrix}\)
- 绕 y 轴:\(\text{rotate-y}(\theta) = \begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}\)
- 绕 z 轴:\(\text{rotate-z}(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
- 剪切:
- 沿 x 轴:\(\text{shear-x}(d_y, d_z) = \begin{bmatrix} 1 & d_y & d_z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
-
任意旋转:三个列向量是相互正交的单位向量。
若沿任意轴 \(\mathbf{a}\) 旋转 \(\phi\),则可以构建基底得到旋转矩阵:\(\begin{bmatrix} x_u & y_v & z_w \\ x_v & y_v & z_w \\ x_w & y_w & z_w \end{bmatrix}\begin{bmatrix} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_u & x_v & x_w \\ y_u & y_v & y_w \\ z_u & z_v & z_w \end{bmatrix}\)。
-
旋转法向量
我们的目标是想要找到,进行旋转 \(M\) 后仍能使 \(\mathbf{Nn}^T\mathbf{Mt}=\mathbf{0}\) 的矩阵 \(N\)。
经过一番推导,得到 \(\mathbf{N} = (\mathbf{M}^{-1})^T\)。
仿射变换¶
Todo
坐标变换¶
Todo
第七章:视图¶
本章解决三维物体到二维屏幕的投影问题。这称为视图变换(view transformation)。这可以看作第四章光线追踪的逆过程。
视图变换¶
涉及相机位置、投影类型、视场、分辨率等。一般被分为三个变换:
- 相机变换(camera transformation):将世界坐标系转换为相机坐标系。取决于相机姿态(pose)。
- 投影变换(projection transformation):将可见的点投影到 \([-1, 1]\) 范围内。取决于投影类型。
- 视口变换(viewport transformation):将 \([-1, 1]\) 范围内的点映射到屏幕上。取决于屏幕大小。
第八章:图像管线¶
第九章:信号处理¶
第十章:表面阴影¶
第十一章:纹理映射¶
第十二章:图形数据结构¶
第十三章:更多光线追踪¶
第十四章:采样¶
第十五章:曲线¶
第十六章:计算机动画¶
第十七章:使用图形硬件¶
第十八章:光照¶
第十九章:色彩¶
第二十章:视觉感知¶
视觉敏感度¶
色彩¶
- 人眼:
- 可视的波长范围从 370nm 到 730nm。
- 视网膜两种光受体(photoreceptor):视锥细胞(cone)负责颜色感知,(rod)负责光强。
- 有三种视锥细胞,对光谱的敏感度不同。
- 光谱的不同分布可以产生相同的颜色。比如 540nm 和 700nm 混合产生的效果与 580nm 无法分辨。
