Skip to content

🏫 控制论

课程简介

  • 学期：2022-2023 学年 春夏学期
  • 课程评定标准：
    • 平时分 50%
      • 每个小组 5-6 人，抽签决定小组 pre 的顺序。
      • 每次理论课后，老师指定一些阅读文献、给出下次讨论课的主题，对应小组准备下次讨论课的内容。
      • 每位同学准备 PPT，讲解时间控制 10-15 分钟，讲解后提问。
      • 每位同学都有 2 次主讲机会。
    • 期末考 50%
      • 开卷，允许参考书、笔记、打印课件。

怎么准备控制论的期末考试？

主要掌握两个内容：

  • 劳斯判据的计算
  • 方框图的计算

其余都靠打印 PPT。

考前一定要浏览一遍历年卷所有题目，PPT 上找不到答案的，就让 ChatGPT 答一遍，如果回答满意的话打印下来，方便直接抄。经济控制论的几道考题都是 PPT 上无法直接找到的，可以这么应对。

22-23 春夏 期末回忆卷

By cc98 blblblb

  1. （10 分）罗伯特·维纳和钱学森是两位著名的控制论科学家，请简述它们对控制论产生和发展过程的代表性贡献。

  2. （15 分）离散时间控制系统需要对模拟信号进行采样、量化得到数字信号。模拟信号为什么需要离散化？若对采样得到的数字信号进行数字滤波，请列举两个数字滤波的方法。ae1ad000e5efbe83

  3. （15 分）右图是行驶状态的两轮自平衡车，请分析自平衡车在静止、行驶过程中的稳定性，道路、环境和操控者自身可能有哪些因素造成行驶过程中稳定性的阻碍？你能够提出哪些可望增强稳定性的做法？

  4. （10 分）列举一个人工生态系统的实例，并分析说明该生态系统的反馈控制或自动调节机制。

  5. （10 分）一个控制系统可以看作是由若干个子系统或单元连接组合而成，请写出子系统或单元连接的几种基本形式。画出一个至少包含 3 种连接方式的控制系统框图。

  6. （15 分）某闭环控制系统框图如下，\(u=6\)，求输出 \(y\) 的表达式。

  1. （10 分）开环传递函数的极点分布有哪几类？判断开环控制系统稳定性的常用方法有哪些？

  2. （15 分）如闭环控制系统特征方程如：\(D(\lambda)=\lambda^4+5\lambda^3+4\lambda^2+7\lambda+6\)，试根据劳思判别法判断该系统的稳定性。

第 1 讲 控制论的基本理论

历年题目

  • 叙述控制论的产生、发展以及核心思想。
  • 列举四个以上对控制论形成和发展有重要推进作用的事件。
  • 列举 3 个以上控制论产生和发展历程中的代表任务及其重要贡献。

第 2 讲 三论

历年题目

  • 简述控制论、系统论、信息论的主要内容和代表任务，并简述这三者的关系。

第 3 讲 控制论的基本方法

本节主要是一些概念性的东西。

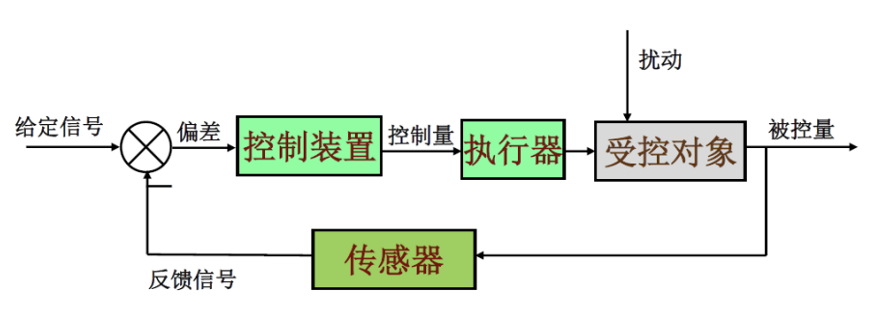
反馈控制

反馈控制的基本结构

  • 反馈控制的特点：
    • 有反馈信息，信号传递形成闭合回路。
    • 抗扰性好，控制精度高。

控制系统建模方法

  • PPT 开头讲了一堆建模的必要性、模型的特点吧啦吧啦。
    • 系统建模的必要性
    • 模型的定义和特征
    • 系统模型的分类
    • 系统模型的分类
    • 系统模型的要求和原则
  • 重点是了解方块图的表示方法。
系统建模的表示方法

其中：\(u(t)\) 是可控制的输入量，\(y(t)\) 是被控的输出量，\(d(s)\) 是不可控制的扰动量。

复杂的系统可以表示为动态模型（大概就是控制量和被控量都随时间这样的其他因素变化吧），从时域、频域、复域角度展开分析。它们的关系如下：

机理建模方法的计算例子

一般步骤：

  1. 确定输入、输出变量
  2. 根据物理定律等写出运动的微分方程
  3. 消去变量，写出输入、输出变量的微分方程
  4. 与输入有关的放在右边，与输出有关的放在左边，按降次排列。

RLC 电路如下图所示：

使用基尔霍夫定律定律得到：

\[ \begin{cases} u(t) = Ri(t) + L\frac{di(t)}{dt} + \frac{1}{C}\int_{0}^{t}i(\tau)d\tau \\ y(t) = i(t) \end{cases} \]

代入得到：

\[ LC\frac{d^2y(t)}{dt^2} + RC\frac{dy(t)}{dt} + y(t) = u(t) \]

这就是这个系统的微分方程模型

机械位移系统如图所示：

使用牛顿第二定律得到：

\[ \begin{cases} F_1=ky(t)\\ F_2=f\frac{dy(t)}{dt}\\ a=\frac{d^2y(t)}{dt^2}\\ F(t)-F_1-F_2=ma \end{cases} \]

整理得到：

\[ m\frac{d^2y(t)}{dt^2}+f\frac{dy(t)}{dt}+ky(t)=F(t) \]

这就是这个系统的微分方程模型

上面的两个例子具有相同的微分方程模型：

\[ a\frac{d^2y(t)}{dt^2}+b\frac{dy(t)}{dt}+cy(t)=u(t) \]
  • 系统越来越庞大，机理建模方法受阻、经验知识积累困难时，我们提出了数据驱动建模方法。PPT 以主元分析法为例进行讲解。
  • 主元分析法首先将多个变量通过数学方法简化为几个综合的统计指标（高维转低维），然后取能反映系统信息量最大的综合指标定义为第一主元。用线性代数进行表述，这是一种优化问题，可以转化为特征值求解问题，需要协方差矩阵的知识。
  • 数据驱动建模方法很有意思，在之后的大数据分析、机器学习、深度学习等课程中会有更多的学习机会。
数据驱动建模方法
  • 统计分析：多元统计分析如主元分析、偏最小二乘等
  • 信号处理：傅里叶变换、谱分析、小波变换方法等
  • 数据挖掘：相关分析、趋势分析、关联规则挖掘、预测分析等
  • 机器学习：聚类方法、分类方法，回归方法，深度学习、强化学习等
  • 其它方法：计算智能方法、仿生计算等

数据建模有这样一个框架：

  • 系统分析法没什么用

第 4 讲 反馈与控制系统

本讲重点

掌握系统的方框图描述。

方框图的基本元素

方框图的基本结构 - 串联和并联
  • 串联：\(G(s) = G_1(s)G_2(s)\)

  • 并联：\(G(s) = G_1(s) + G_2(s)\)

方框图的基本结构 - 反馈

  • 负反馈系统：\(Y=(\frac{G}{1+GH})U\)
  • 正反馈系统：\(Y=(\frac{G}{1-GH})U\)（就是求和点变号了而已）
为什么反馈控制好？

方块图化简 - 点的移动

向前移动：\(Hs\)，向后移动：\(\frac{1}{H}s\)

相邻求和点可任意换位。

向前移动：\(\frac{1}{H}s\)，向后移动：\(Hs\)

相邻引出点也可任意换位。

例题：求解输出与输入的关系

  • 信号流图大概就是把方框图的方框画成线就是了。
  • 如果出现信号流图，它所表示的系统很可能比较复杂，需要使用梅逊增益公式进行化简。
信号流图的结构

历年题目中没有出现只能使用梅逊公式化简的题目，所以这里就不讲了。

历年题目

  • 计算下面信息流的总增益：
  • 从系统论的整体性、关联性、动态平衡性、时序性等基本特征出发，简要分析如图所示的单闭环反馈控制系统image-20230619163647121
  • 反馈系统如下图所示，若 \(u=3\)，求 \(y\)。
  • 某系统框图如下，输入 \(u=4\)，求输出 \(y\) 的表达式
  • 某系统框图如上图，输入 \(u=2\)，试求输出 \(y\) 的表达式。
  • 一个控制系统可以看作是由若干个子系统或单元连接组合而成，请写出子系统或单元连接的几种基本形式。

第 5 讲 稳定性

本讲摘要

本讲的上下限差距也拉得很大，前面讲一堆废话，后面“硬核选学”部分又需要非常深厚的数学功底，涉及线性系统得稳定性分析等大量的代数学内容。反正我学完整门课都没搞懂拉式变换。

历年题目：

  • 钱学森为什么可以创立《工程控制论》？它与维纳的《控制论》区别与联系？

第 6 讲 时域分析

本讲摘要

从本讲开始，我们接触到控制论在理工科的核心应用——控制系统的分析与设计。我们从基本的控制系统时域和频域分析开始，再到信号与通信，最后到 PID 控制——最为泛用的反馈控制器。

本讲的重点是掌握控制系统的时域分析方法 - 概念性内容：包括阶跃响应、脉冲响应、频率响应、稳态误差等。 - 计算性内容：劳斯判据

典型的输入信号

几种典型信号

控制系统的稳态误差和动态品质

阶跃输入引发的输出调节过程的动态品质指标

在上图中，有几个重要的指标： - 稳态误差 \(\delta(\infty)\) - 最大超调量 \(\sigma_p=\frac{y(t_p)-y(\infty)}{y(\infty)}\)：响应曲线偏离稳态值得最大值，百分比表示。说明系统得相对稳定性 - 延滞时间 \(t_d\)：到达稳态值 50% 所需时间 - 峰值时间 \(t_p\)：到达第一个峰值（最大超调量）所需时间 - 上升时间 \(t_r\)：多种定义，以下都是相对于稳态值的百分比 - 从 10% 到 90% 的时间（适用于无振荡的系统） - 从 5% 到 95% 的时间 - 从 0 到 100% 的时间（适用于有振荡的系统） - 调整时间 \(t_s\)：从 0 到进入稳态值在 95%~105% 的时间

线性控制系统的微分方程模型

加热电炉的数学模型及其推导

看 PPT 吧。

求解线性控制系统的微分方程模型

线性常系数微分方程的解

线性常系数微分方程的解是由微分方程的一个特解加上齐次微分方程的通解得到的。

通常取系统的稳态解作为特解，齐次微分方程的通解为暂态解。

从微分方程看系统的稳态

如果特征根是负数，或具有负实部，那么系统的稳态解是收敛的，换言之系统是稳定的；否则就是不稳定的。

劳斯判据

  • 劳斯判据的本质是判断系统的极点是否在右半平面，如果在右半平面，那么系统就不稳定。
劳斯的代数稳定判据
  1. 按降次幂列出闭环控制系统的特征方程式
\[ D(\lambda)=a_n\lambda^n+a_{n-1}\lambda^{n-1}+\cdots+a_1\lambda+a_0=0 \]
  1. 根据系数列出劳斯表
\[ \begin{array}{c|c|c|c|c|c} \lambda^n & a_n & a_{n-2} & a_{n-4} & \cdots & a_0 \\ \lambda^{n-1} & a_{n-1} & a_{n-3} & a_{n-5} & \cdots & 0 \\ \lambda^{n-2} & b_1 & b_2 & b_3 & \cdots & 0 \\ \lambda^{n-3} & c_1 & c_2 & c_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \lambda^1 & e_1 & e_2 & e_3 & \cdots & 0 \\ \lambda^0 & f_1 & f_2 & f_3 & \cdots & 0 \\ \end{array} \]
  1. 从第三行起，各元素按下列公式计算，直到求出 \(n+1\) 行。
\[ \begin{aligned} b_1 &=\frac{-\left|\begin{array}{cc}a_{n} & a_{n-2} \\ a_{n-1} & a_{n-3}\end{array}\right|}{a_{n-1}} \\ b_2 &=\frac{-\left|\begin{array}{cc}a_{n} & a_{n-4} \\ a_{n-1} & a_{n-5}\end{array}\right|}{a_{n-1}} \\ c_1 &=\frac{-\left|\begin{array}{cc}a_{n-1} & a_{n-3} \\ b_{1} & b_{2}\end{array}\right|}{b_1} \\ c_2 &=\frac{-\left|\begin{array}{cc}a_{n-1} & a_{n-5} \\ b_{1} & b_{3}\end{array}\right|}{b_1} \\ \end{aligned} \]
  1. 线性定常闭环控制系统稳定的充分必要条件：微分方程特征方程式系数均为正，劳斯表中第一列所有系数均为正。
劳斯判据例题

历年题目

  • 根据炉温控制系统判断被控变量，控制变量，如何对系统进行时域分析？

  • 闭环控制系统特征方程如下，用劳斯判据判断其稳定性

    \[ D(\lambda) = \lambda^4+6\lambda^3+9\lambda^2+8\lambda+6=0 \]

  • 闭环控制系统特征方程如下，用劳斯判据判断其稳定性

    \[ D(\lambda) = 2\lambda^4+5\lambda^3+4\lambda^2+7\lambda+1=0 \]

第 7 讲 频域分析

第 8 讲 离散时间控制

历年题目：

  • 控制系统中的模拟型号、离散信号、数字信号之间有什么区别和联系？时间连续信号为什么要离散化？通过采样实现时间离散化后的数字系统是否能够还原为原先的连续系统？

第 9 讲 PID 控制

历年题目：

  • 叙述 PID 控制中 P、I、D 的含义，一般表达式及实际应用
  • 简要解释 PID 控制器中参数 KP、KI、KD 的作用，谈谈针对复杂的应用环境 PID 控制器有什么改进或拓展。
  • 叙述 PID 控制中 P、I、D 的含义，一般表达式，举例说明 PID 控制器的作用。

第 10 讲 机器人及其控制技术

历年题目：

  • 【3 次】火箭在海上着陆平台进行垂直着陆，影响火箭着陆稳定性的因素有哪些？可以通过什么措施提高稳定性？
  • 简述机器人的基本构成与控制方式

第 11 讲 自主车辆与交通控制

历年题目：

  • 城市交通控制的目的有哪些？智慧城市交通系统中有哪些控制技术？

第 12 讲 智能制造中的控制

历年题目：

  • 请分析工业大数据与互联网大数据在数据来源、应用价值等方面的区别。
  • 工业 4.0 和人工智能的关键词都是“智能”，谈一谈工业智能和一般人工智能的连续与区别？
  • 简述工业大数据与互联网大数据的主要区别，并说明工业大数据和智能制造有什么关系？

第 13 讲 先进控制

第 14 讲 经济控制

历年题目：

  • 根据下面框图分析闭环经济控制
  • 分析下面国民经济反馈控制系统体现出的基本控制思想，并说明该系统中给定值、控制作用和扰动具体是什么？
  • 在上面的国民经济反馈控制系统中，列举三种以上的扰动作用，并分析如何克服扰动作用的不良影响。

第 15 讲 生物控制论

历年题目：

  • 试叙述人体站立稳定性的定义，分析为什么蒙住双眼和单腿站立时稳定性会下降？